Nate Atkinson, Scott Ganz and I have co-authored a new article, to be published in the Illinois Law Review, and now posted on SSRN in its current draft. The article is based on computer simulations that Nate and Scott conducted comparing (1) Alaska’s new “top four” electoral system, which uses the “instant runoff” form of ranked-choice voting, and (2) a variation on Alaska’s system that substitutes a “Condorcet-compliant” method of ranked-choice voting instead of the instant runoff version. A “Condorcet-complaint” electoral system is one that elects a candidate whom a majority of voters prefers to each other candidate when candidates are paired against each other head-to-head.
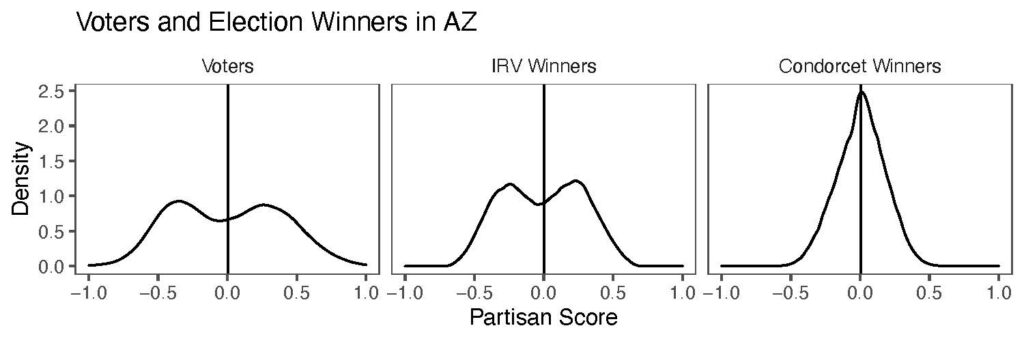
Nate and Scott created a profile of the electorate of each state, using Cooperative Election Study data. Interestingly, states differ significantly in the degree to which their electorates are polarized. Some states, for example, have a bimodal distribution of voters as a result of polarization. Other states, by contrast, have a distribution of voters that is unimodal, resembling a more conventional “Bell Curve”.
Nate and Scott then simulated 250,000 four-candidate elections for each state, using both “instant runoff” and “Condorcet-compliant” versions of ranked-choice voting. The results are striking. In all states, Condorcet-compliant RCV tends to elect a candidate whose position in the distribution of the electorate is closer to the electorate’s median voter than instant-runoff RCV will. The difference between the two forms of RCV, however, is significantly greater in those states with a polarized bimodal distribution of voters. In those states, the gap between the instant runoff winner and median voter compared to the corresponding gap between the Condorcet winner and the median voter is much larger.
The paper includes graphs showing these results for all fifty states. As an illustration, here (from left to right) are the electorate profile, instant runoff winners, and Condorcet winners for Arizona, one of the states with a polarized bimodal distribution: