Yesterday I laid out a series of criteria that, Eric McGhee and I argue in a forthcoming article, can be used to evaluate measures of partisan gerrymandering. Today I’ll briefly explain why the efficiency gap satisfies these criteria.
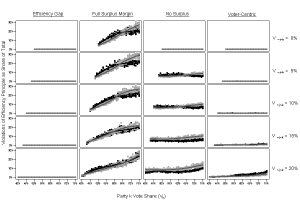
Start with the principle that if a party wins more seats with the same votes, a metric should indicate a larger advantage for this party. To test the efficiency gap’s compliance with this principle, we simulated thousands of district plans. In these simulations, we allowed the major parties’ vote shares to vary from 25% to 75%, a third party’s vote share to range from 0% to 20%, and turnout to diverge across districts by up to a factor of 15. The results of the simulations are below (for both the efficiency gap and several variants that scholars have proposed). It’s immediately evident that the efficiency gap never violates the principle. In every electoral setting, the efficiency gap moves in the correct direction when a party secures more seats without appealing to more voters.
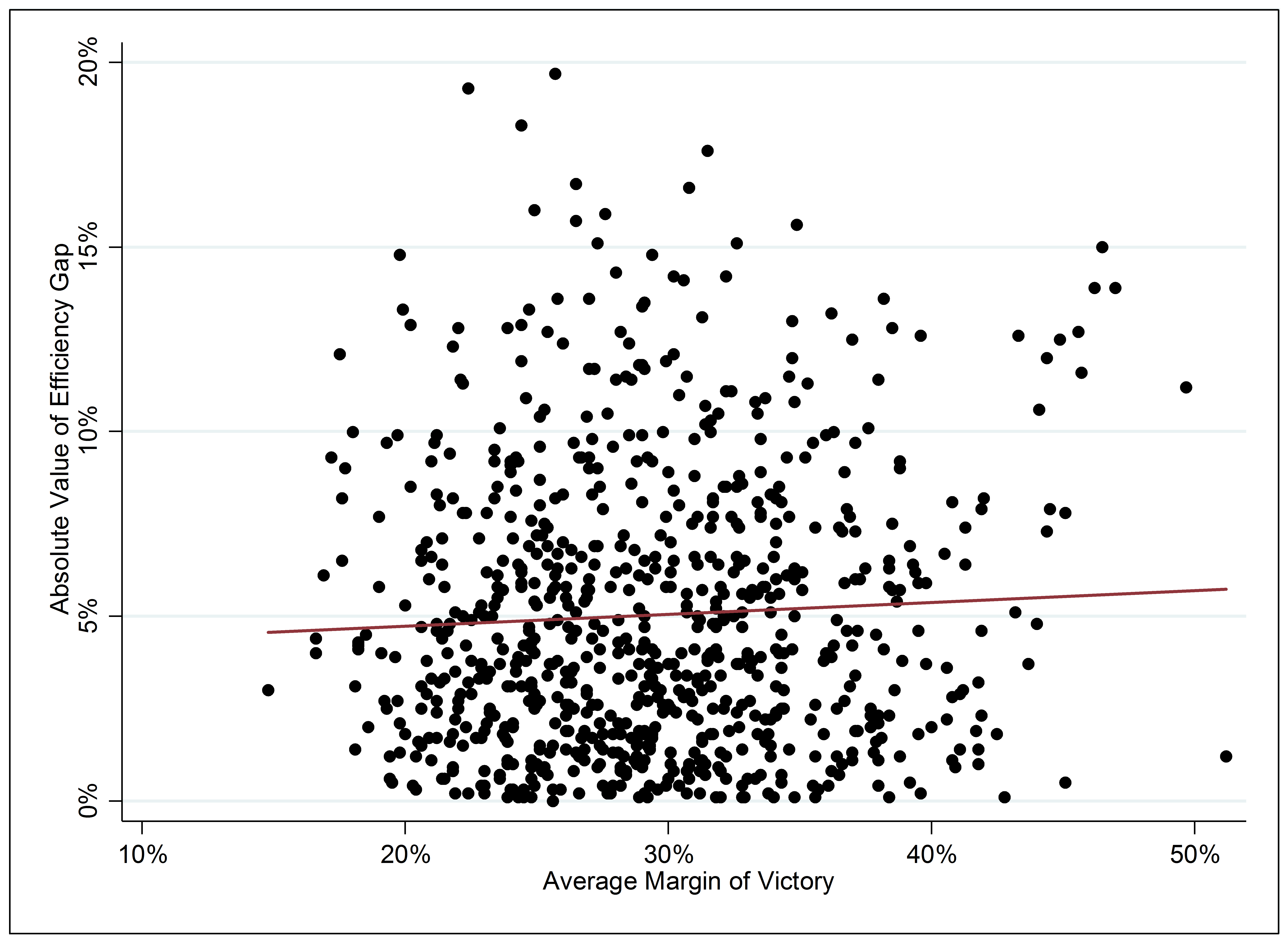
Next, consider the efficiency gap’s distinctness from other electoral values—competitiveness in particular, which some have claimed is related to the measure. Conceptually there’s no connection because it’s the difference between the parties’ average margins of victory (not the average margin itself) that drives the efficiency gap. Empirically too, as the below chart illustrates for state houses from 1972 to 2014, the correlation between the efficiency gap and the average margin of victory in an election is zero. In other words, knowing how competitive a state’s districts are tells us nothing about how skewed they are in favor of a party.
Third, the efficiency gap can be (sensibly) calculated in a wide range of electoral environments. Safe states pose no problem for the metric; it’s just as meaningful in, say, Massachusetts as in Michigan. Turnout variations from district to district aren’t an issue either; in fact, they’re directly incorporated into the wasted vote tallies that are used to compute the efficiency gap. And while we originally presented a two-party version of the efficiency gap, our article shows how it can be extended to the multiparty context.
Lastly, the efficiency gap is highly consistent with American electoral history. The below chart is a density curve of state house efficiency gaps from 1972 to 2014. The distribution is a near-textbook bell curve, centered almost exactly at zero. Most prior maps have thus been symmetric in their treatment of the major parties, and highly skewed plans have been rare. There also is no hint that the country’s political geography is tilted in either party’s direction. If it were, then the distribution’s mean and median would not be so close to perfect symmetry.