Yesterday I pointed out that the efficiency gap complies with a series of criteria that, Eric McGhee and I argue in a forthcoming article, can be used to evaluate measures of partisan gerrymandering. To determine if the same is true of other metrics, we simulated several thousand more district plans, allowing the major parties’ vote shares to vary between 25% and 75%. The below charts show how often partisan bias (on the left) and the mean-median difference (on the right) violate the principle that if a party wins more seats with the same votes, a measure should indicate a larger advantage for this party. Party vote share is on the x-axis; the frequency of violations of this principle is on the y-axis.

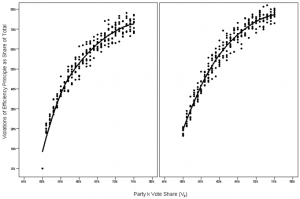
In competitive jurisdictions, where the statewide vote is close to split, partisan bias and the mean-median difference perform reasonably well. They infrequently show a party scoring the same (or worse) while winning more seats with the same votes. But in uncompetitive jurisdictions, where one party predominates statewide, violations of the principle rise sharply. By the time one party earns 60% of the statewide vote, partisan bias and the mean-median difference produce counterintuitive results about half the time.

To see if this analysis has real-world implications, we constructed a series of regression models. The dependent variable in each case is the average ideology of a state’s House members in a given term. The key independent variable is a measure of partisan gerrymandering: the efficiency gap, partisan bias, or the mean-median difference. And we ran separate models for each metric and for competitive elections (closer than 55%-45% statewide) and uncompetitive elections (further apart than 55%-45%).

The below chart displays the results of these models. Each point indicates the impact on a congressional delegation’s average ideology of increasing a particular gerrymandering metric by one standard deviation. It is apparent that in competitive electoral settings, all three measures have large and statistically significant effects. If a swing state’s efficiency gap, partisan bias, or mean-median difference becomes more pro-Democratic (or pro-Republican), the state’s delegation becomes more liberal (or conservative) on net. But in uncompetitive environments, only the efficiency gap remains statistically significant. It continues to show that gerrymandering influences congressional representation. Partisan bias and the mean-median difference, on the other hand, wrongly suggest that gerrymandering in safe states has no impact on delegations’ ideological makeups.

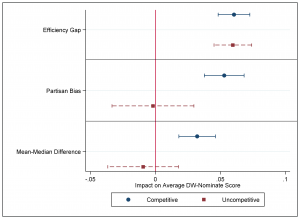
The conclusion we draw from these studies is that in the competitive states where most recent partisan gerrymandering lawsuits have been filed (e.g., North Carolina, Pennsylvania, Wisconsin), all of the common gerrymandering metrics can and should be used. But if scholars or litigants want to analyze gerrymandering in uncompetitive states, they should not use partisan bias or the mean-median difference. These measures frequently violate the seat-vote principle in these settings, and are no longer connected to the substantive value—the quality of representation—that gerrymandering offends.